Learning to Program – A Beginners Guide – Part Nine – Introducing Functions in F#

In the last section we took a first look at logic, and started to build up some quite complex expressions. We noted that it would be useful if we could somehow bind those expressions to a shorthand so that we didn't have to keep typing them all out every time we wanted to use them (which is tedious, and prone to error.)
This is where functions come in.
A function is the smallest useful unit of program, that takes exactly one input, and transforms it into exactly one output. Here's a block diagram to represent that.
(It's worth noting that when we're talking about inputs and outputs in the context of a function, these aren't the I/O operations of our block diagram back in the simple model of a computer - the keyboards, monitors, printers and so forth. The input is just a parameter of the function and the output is its result.)
As usual, there are lots of ways of describing a function. You might have seen this block diagram expressed in a more compact mathematical form:
\(x \mapsto f(x)\ \)
You can read that as 'x' 'goes to' 'f-of-x'. Mapping that on to the diagram above, you can see that x is the input parameter, f is our function, and f(x) is our output - the result of applying the function f to x.
Let's get more specific. How could we describe a function whose result is the value of the input, plus 1?
\(x \mapsto x+1\ \)
So, as you might expect, you can read that as 'x' 'goes to' 'x plus 1'. And by observation, we can say that
\(f(x)=x+1\ \)
So, that's the block diagram and the general mathematical form. What about some code?
Defining functions in F#
Different programming languages have all sorts of different ways of defining a function. We're going to focus on F# for our examples. The syntax may vary from language to language, but the principles are the same. If you learn the principles, you can apply that knowledge to any code you come across.
It's not just different languages that introduce some variety in to the way you can define a function, though. There are lots of ways of defining a function in F#, depending on the context. We're going to avoid some of that detail, for the time being, and start out with a simple example, where we define a function and bind it to an identifier, so that we can call it as often as we like.
There's a lot of seemingly innocuous English words in that last sentence, like 'call' and 'bind'. But what does it actually mean?
We say that we call a function when we give it an input, and ask it to evaluate the output for us.
An identifier is a named value, and when we bind a function (or other value) to an identifier, we associate the name with that function or value (forever!).
Here's a simple example of a binding in F#. You can start up your F# runtime environment (fsi or fsharpi) and try it out.
let x = 3
(don't forget to type ;; when you want the runtime to evaluate your input.)
So, the syntax for a binding is as follows:
let {identifier} = {value}
F# responds with
val x : int = 3
You can read the result as 'the value called x is a 32-bit integer which equals 3'.
What about this notion of a binding being forever? Let's experiment with that by binding 3 to the identifier y, and then trying to bind 4 to that same identifier.
let y = 3
let y = 4
We want F# to evaluate both of these lines as a block, so we type the first line, press return, and type the second line, before typing our usual ;; to kick off the evaluation.
F# responds with
let x = 4
----^
stdin(4,5): error FS0037: Duplicate definition of value 'x'
This tells us that F# is not happy. Our second attempt to bind the identifier x was an error. It has even drawn a handy arrow to the bit of our statement that was wrong. You'll get very familiar with F# errors before we're done!
We don't have to bind a simple value to an identifier, though, we can bind a function, too.
Remember that when we bind a simple value to an identifier, we use the syntax
let {identifier} = {value}
But to bind a function to an identifier, we need to include a name for the input parameter too, so we use the syntax
let {identifier} {parameter} = {function body}
Let's try it:
let increment x = x + 1
F# responds with:
val increment : x:int -> int
We can read that as 'the value called increment is a function which takes a 32-bit integer (called x, as it happens), and goes to a 32bit integer.'
We can then use the function. F# applies a function (increment, in this case) to the value immediately to its right, which it uses as its input parameter.
increment 3
F# responds:
val it : int = 4
Spot test: We learned how to read that kind of response in the previous section. What does it mean?
Answer: The result ('the value called it') is a 32 bit integer which equals 4.
So far so good! We've created our first function.
A function doesn't have to map its input to a number, though. One thing we could return from a function is another function. Let's have a look at an example of that.
let add x = fun y -> x + y
If we execute that line, F# responds with:
val add : x:int -> y:int -> int
Can we read that? The value called add is a function which takes a 32 bit integer called x, and returns a function which takes a 32 bit integer called y, which returns a 32bit integer.
It's a bit long winded, but it's quite straightforward if you follow it through, carefully. Read it a couple of times and see how it matches up with the F# response above.
Hang on a minute, you may be thinking. How exactly did we define the function that was returned? Let's remind ourselves of the syntax for binding a function to an identifier again.
let {identifier} {parameter} = {function body}
In this case, the function body itself returns a new function. By inspection, this must be the code which defines the new function that form the result:
fun y -> x + y
First, you can see that we are clearly not binding this function to an identifier. There's nothing to say we couldn't - we just haven't. Secondly, we're using a different syntax to define the function. We call this new syntax a lambda.
Compare it with the maths-y way of defining a function we looked at right at the beginning of this section
\(y \mapsto x+y\ \)
It's remarkably similar, but, as there isn't an \(\mapsto\ \) key on our computer, the designers of F# have used -> as a cute replacement. We also add the prefix fun to tell F# that we are starting to define a function.
So, how do we read it?
fun y -> x + y
This means 'a function which takes a parameter called y, and goes to some value x plus y'.
This seems to be a bit lacking in information. Where do we get the x from, for a start?
Remember that our whole definition was:
let add x = fun y -> x + y
We say that the lambda function is being defined in the scope of the definition of the add function, or that the add function is the parent (or an outer) scope of the lambda (which is, conversely, a child or an inner scope of the add function). You can think of scopes like a series of nested boxes. An inner scope has access to the identifiers defined in any outer scope which contains it, but an outer scope cannot reach into an inner scope and rummage in its innards.
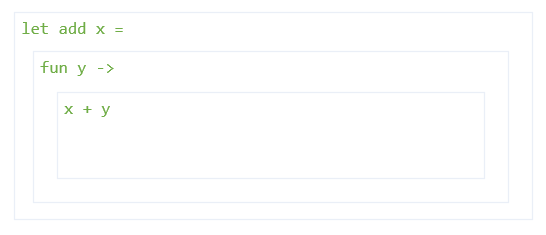
So, our lambda gets its x value from the outer scope - the parameter to the add function.
And what about an identifier for this function? Well, it doesn't have one. We've not bound it to an identifier anywhere. We call this an anonymous function. Why doesn't it have a identifier? Well, it doesn't really need one. As we said above, there's no way to 'reach inside' the body of the function and fish it out, so we don't need to bother binding it to an identifier when we define it.
As we mentioned before, there's nothing to stop us binding it to an identifier along the way, if it would make our code clearer. Here's an example of that
let add x =
let inner = fun y ->
x + y
inner
Notice how the function body now extends over several lines, so we've had to indent it with spaces to tell the F# compiler that you should treat this all as a single block. If you look back up at our box diagram for the scopes, you can see that it looks quite similar - we just haven't drawn the boxes! We're still creating a lambda, but binding it to an identifier called inner, and then returning the value of that identifier, rather than the returning the lambda directly.
Quick note: You might be tempted to use a tab to indent it neatly- that won't work. F# requires that you use spaces. If you're using an editor to write your F# code, make sure you have set it to "convert tabs to spaces" mode, and then you can hit the tab key to indent.
That's a lot more verbose, and, in such a simple example, not really any clearer, so we'll prefer the definition in our original form.
let add x = fun y -> x + y
A note on style
In earlier sections, we talked about the fact that the choices you make when you choose how to implement an algorithm can influence the cost of that algorithm quite significantly - be that in terms of program length, memory consumption or computational effort. But there's another way in which your choice of implementation can affect the system, and that's in how easy it is to understand.
We may spend a long time carefully crafting some code, but if we come back to that code later and can't work out how it works by looking at it, then we may misinterpret what it does, or how to set it up, or what its constraints might be. This is a rich source of errors in our programs! So, unless there is some absolutely critical reason why we shouldn't (and there almost never is), we prefer to use short, simple functions with a minimum of extraneous detail, that do exactly one thing, and without side-effects in the rest of the system.
Ok so we've created a function that returns a function. What earthly use is that? Well, one way we can use it is to create a whole family of functions.
Try the following
let add1 = add 1
Spot test: What do you think F# is going to respond? Try and work it out before you look below.
Hint: We're binding something to an identifier called add1, and the body of the binding is a call to the add function we just defined, where the value passed as the parameter called x is 1. Remember that the add function returns another function.
Answer:
val add1 : (int -> int)
We know that we can read that as "the identifier add1 is bound to a function that takes a 32bit integer, and returns a 32bit integer".
Let's try another
let add2 = add 2
What's F# going to respond?
val add2 : (int -> int)
Clearly, we could do this for any arbitrary integer we wanted.
And how do we use any of these functions we're creating? Well, add2 is an identifier bound to a function which takes an integer, and returns an integer, so there's no magic to that.
Spot test: How would we use this function to calculate 2 + 3?
Answer:
add2 3
val it : int = 5
Spot test: What is 3657936 + 224890?
Hint: Don't use your calculator! Use our fabulous integer addition function factory!
Answer:
let add3657936 = add 3657936
add3657936 224890
F# responds with
val add3657936 : (int -> int)
val it : int = 3882826
In fact, we can leave out that intermediate function binding entirely.
Try the following:
add 3 4
F# responds with
val it : int = 7
Excellent! But how did that work?
Well, remember that F# applies a function to the value immediately to its right, which it uses as the parameter to the function.
First, it applied the add function to the value to its right (the 32bit integer 3) and that, as you know, returns another function. So it took that resulting function and applied it to the value to its right (the 32bit integer 4), resulting in our answer: 7.
This is a very interesting result. The net effect is that we can add any two numbers together, even though any given function can only take one input, and produce one result, by using a function that returns a function.
This is such a useful pattern (and writing it all out by hand is a bit of a drag) that F# gives us a shorthand.
Instead of
let add x = fun y -> x + y
We can type
let add x y = x + y
F# responds
val add : x:int -> y:int -> int
Notice that this is exactly the same as our original definition - the value called add is a function that takes a 32bit integer and returns a function that takes a 32bit integer and returns an int.
And we can still type
add 3 4
to get
val it : int = 7
In this new shorthand syntax, we can just think of the function as taking several parameters - two in this case - but we know that what is really happening under the covers is that we are creating a function that takes the first parameter, and returns a function that takes the second parameter (and uses the first parameter, from the outer scope, in its body).
And if we need to, we can still capture that intermediate function, with its first parameter bound to a particular value.
let add342 = add 342
val add342 : (int -> int)
We call this binding of a subset of the parameters of a function currying and we'll learn more about that in a later section.
Exercise: Create a function that applies the logical XOR operator we worked out in the previous section.
In the next section we'll look at the answer to that exercise, and how we can make the function work more like the other logical F# operators we've already used.




